|
|
|
|
|
Egyenletek, egyenlőtlenségek grafikus megoldásakor az egyenlet,
egyenlőtlenség két oldalát két, képlettel megadott függvényként kezeljük. A
megoldás során az alaphalmaznak azokat az elemeit keressük, amelyeket a két
képletbe helyettesítve, teljesül az így kapott függvényértékekre az egyenlőség, illetve az
egyenlőtlenség. A keresést a függvények grafikus ábrázolásával végezzük. |
|
Példa |
|
1. |
|
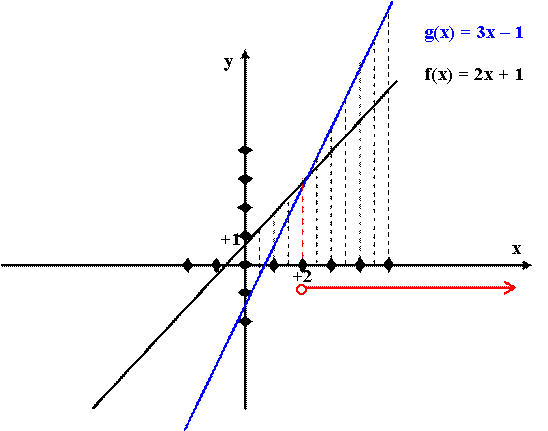
Oldjuk meg grafikusan a
következő egyenletet! 2x + 1 = 3x – 1 A baloldal: f(x) = 2x + 1 — egy
elsőfokú, lineáris függvény képlete A jobboldal: g(x) = 3x – 1 —
egy elsőfokú, lineáris függvény képlete |
|
|
|
Az alaphalmaznak azt az x
elemét keressük, amelynek a képe mindkét függvény esetében ugyanaz a szám. Ábrázoljuk a két függvényt közös koordináta-rendszerben! |
|
|
|
|
|
|
|
A grafikonról leolvasható, hogy az
alaphalmaz x = 2 értékéhez mindkét függvény ugyanazt a függvényértéket
rendeli. Az egyenlet megoldása: x = 2 |
|
2. |
|
|
|
Oldjuk meg grafikusan a
következő egyenlőtlenséget! 2x + 1 < 3x – 1 Ezúttal az alaphalmaznak
azokat az elemeit keressük, amelyekhez az f(x)
képlettel megadott függvény kisebb függvényértékeket rendel, mint a g(x)
képlettel megadott függvény. |
|
|
|
|
|
|
|
A szaggatott vonalak segítségével észrevehető, hogy az alaphalmaz +2-nél nagyobb elemeihez rendel az f függvény
kisebb számokat a képhalmaz elemei közül, mint a g függvény. Az egyenlőtlenség megoldása: x > 2 |
|
|
|
3. |
|
|
|
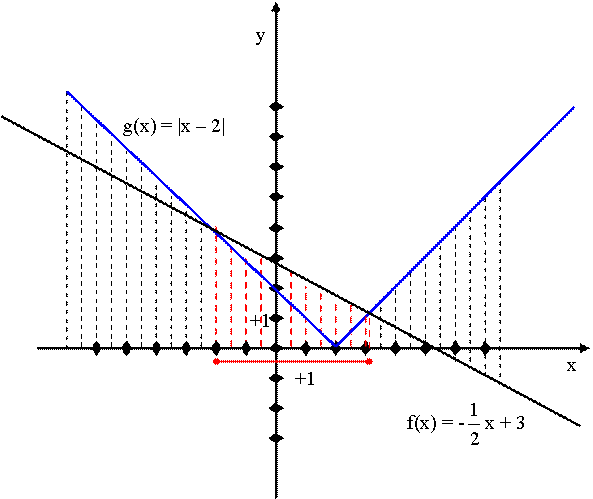
Oldjuk meg grafikusan a
következő egyenlőtlenséget! - A baloldal: f(x) = - A jobboldal: g(x) = |x – 2| — egy abszolút érték függvény képlete |
|
|
|
|
|
|
|
A grafikonokról leolvasható,
hogy az f függvény az alaphalmaz -2-nél nem kisebb,
de +3,3–nél nem nagyobb értékeihez rendel nagyobb, vagy ugyanakkora
függvényértékeket, mint a g függvény. Az egyenlőtlenség megoldása: -2 ≤ x ≤
3,3 Ezek csak közelítő értékek,
mert a grafikus megoldás hátránya a pontatlanság, most is tapasztalható. Általában olyan egyenletek
megoldásánál használjuk a grafikus megoldást, amelyeket algebrai úton nem,
vagy csak nagyon bonyolultan lehet megoldani. |
|
|