|
|
||
|
|
||
|
|
||
|
Az f
függvény monoton növekvő az értelmezési tartomány
valamely H részhalmazán, ha a H halmaz bármely két (x1, x2)
elemére teljesül: ha x1 < x2, akkor
f(x1) £ f(x2). (Növekvő független változókhoz növekvő függvényértékek
tartoznak.) Az f
függvény monoton csökkenő az
értelmezési tartomány valamely H részhalmazán, ha a H halmaz bármely két (x1,
x2) elemére teljesül: ha x1 < x2, akkor
f(x1) ³ f(x2). (Növekvő független változókhoz csökkenő függvényértékek
tartoznak.) |
||
|
|
||
|
Intervallum (számköz): a számegyenes egy szakasza. Két
végpontja közötti számok halmaza. A végpontjaihoz tartozó számokról nevezzük
el. |
||
|
|
||
|
[4; 9] intervallum [-7; 2,6] intervallum [a; b] intervallum |
|
Zárt intervallumok. A végpontok is
beletartoznak a számhalmazba. (Zártságát a zárójelek jelzik:[ ] ) |
|
|
||
|
]-4; 3[ intervallum ]4,7; 18[ intervallum vagy (-4; 3)
intervallum (4,7;18) intervallum |
|
Nyitott intervallumok. A végpontok nem
tartoznak bele a számhalmazba. (Nyitottságát a zárójelek jelzik: ] [ vagy ( ) ) |
|
|
||
|
Az f függvény értelmezési tartományának x0
pontja maximumhely, ha a hozzá
tartozó függvényérték, f(x0) az értékkészlet
legnagyobb eleme. Az f(x0) értéket a függvény maximumának nevezzük. Minden x ÎÉTf esetén
f(x) < f(x0) Az f függvény értelmezési tartományának x0
pontja minimumhely, ha a hozzá
tartozó függvényérték, f(x0) az értékkészlet
legkisebb eleme. Az f(x0) értéket a függvény minimumának nevezzük. Minden x ÎÉTf esetén
f(x)
> f(x0) A függvény maximumát és
minimumát közös néven a függvény szélsőértékeinek
nevezzük. |
||
|
|
||
|
Az f függvény értelmezési tartományának x0
pontja zérushely,
ha a hozzá tartozó függvényérték 0, azaz f(x0)
= 0. Ebben a pontban metszi, vagy érinti a függvény grafikonja az x tengelyt. |
||
|
|
||
|
A függvényvizsgálat lépései
az általános iskolában: |
||
|
|
||
|
1. A függvény értelmezési
tartományának meghatározása. ÉT (Ha nincs megadva.) 2. A függvény értékkészletének
meghatározása. ÉK 3. A függvény zérushelyeinek
meghatározása. 4. A függvény monotonitásának
vizsgálata. Monoton
növekvő: az intervallumok megadása. Monoton
csökkenő: az intervallumok megadása. 5. Szélsőértékek meghatározása: Maximumhely,
maximum. Minimumhely,
minimum. |
||
|
|
||
|
Példa |
||
|
|
||
|
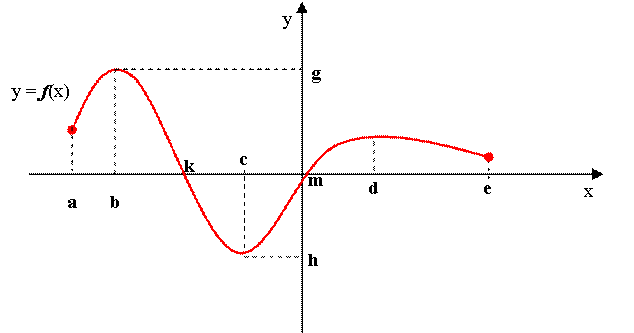
Vizsgáljuk a grafikonjával
adott f valós függvényt a megadott szempontok szerint! |
||
|
|
||
|
|
||
|
|
||
|
|
||
|
1. ÉTf:
[a; e] Másképp megadva: a £ ÉTf £ e 2. ÉKf:
[h; g] Másképp megadva: h £ ÉKf £ g 3. Zérushely: x = k, x = m 4. a. A függvény monoton növekvő: [a; b] [h; d] b. A függvény monoton csökkenő: [b; h] [d; e] 5. c. Maximumhely: x = b, maximum: f(b)
= g d. Minimumhely: x = c, minimum: f(c) = h |
||