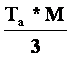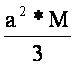Ötszög alapú szabályos gúla
A gúlát egy sokszög, és annyi háromszög határolja, ahány oldalú a sokszög. A sokszög a gúla alaplapja, a háromszögek a gúla oldallapjai. Az alaplapot határoló élek az alapélek. Az oldallapok az oldalélekben találkoznak. Az oldalélek egy pontban, a gúla csúcspontjában futnak össze. Az oldallapok együtt a gúla palástját alkotják. A gúla magassága a gúla csúcsa és az alaplap síkjának a távolsága, vagyis a csúcsból az alaplap síkjára állított merőleges szakasz hossza. Ha a gúla alaplapja szabályos sokszög, és a magasságának talppontja az alaplap középpontjában van, akkor szabályos gúlának nevezzük. A háromoldalú gúla neve: tetraéder. A szabályos tetraéder olyan gúla, amelynek minden lapja szabályos háromszög. A gúla felszíne az alaplap területének (Ta) és az oldallapok területének, vagyis a palást területének (Tp) az összege: A = Ta + Tp. A gúla térfogata az alaplapjával és a testmagasságával megegyező alaplapú és magasságú hasáb térfogatának a harmada: V =
A gúla hálója egy sokszögből, és annyi háromszögből áll, ahány oldalú a gúla.
A szabályos ötszög alapú gúla egy lehetséges hálója.
Négyzet alapú szabályos gúla
	A négyzet alapú szabályos gúla felszíne: A =a^2 + 2*a*m A négyzet alapú szabályos gúla térfogata: V =
Ötszög alapú gúlák