|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
Ötszög alapú egyenes hasáb |
|||||
|
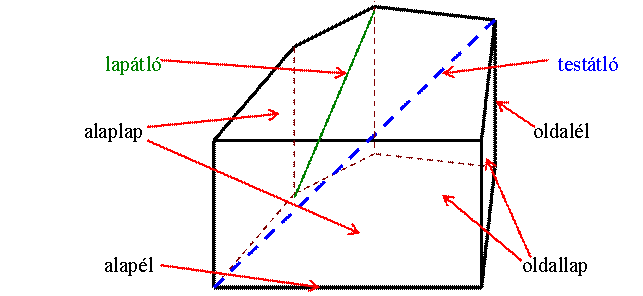
Az egyenes hasáb: olyan test, amelyet két
párhuzamos, egybevágó sokszöglap és annyi téglalap határol, ahány oldala van
a sokszögnek. A két párhuzamos, egybevágó sokszög a hasáb alaplapja. A többi lap a hasáb oldallapja.
Az oldallapok együtt a hasáb palástját
alkotják. Az egyenes hasáb oldalélei merőlegesek az alapra. Lapátló:
két, egy lapon lévő, nem szomszédos csúcsot összekötő egyenes szakasz. Testátló:
két, nem egy lapon lévő csúcsot összekötő egyenes szakasz. Magasság: A
két alaplap síkjának távolsága az egyenes hasáb magassága. A magasság
megegyezik az oldalél hosszával. A hasáb felszíne a
határoló lapok területének, azaz az alaplapok területének (Ta) és a palást területének (Tp) az összege: A
= 2Ta + Tp A hasáb hálóját
kapjuk, ha a hasábot határoló felületet a síkban kiterítjük. Ennek területe
egyenlő a hasáb felszínével. A hasáb térfogata:
alaplap területe * testmagasság: V = Ta * m |
|||||
|
|
|||||
|
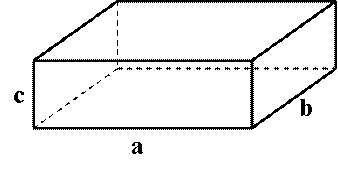
TÉGLATEST Olyan egyenes hasáb, amelynek alaplapja
téglalap. (Minden lapja téglalap.) |
|||||
|
|
|
|
|||
|
|
|
|
|||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
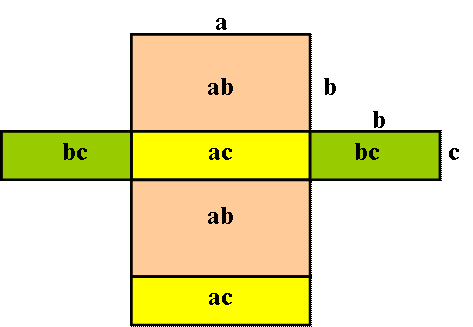
A téglatest egy lehetséges hálója. |
|||||
|
|
A
téglatest felszíne: A = 2(ab + ac
+ bc) A
téglatest térfogata: V =
abc |
|
|||
|
|
|||||
|
|
|||||
|
|
|||||
|
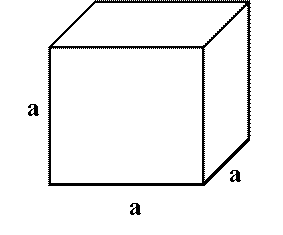
KOCKA Olyan téglatest,
amelynek minden éle egyenlő. |
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
A kocka egy lehetséges hálója. |
|||||
|
|
|||||
|
|
A
kocka felszíne: A = 6 a2 A
kocka térfogata: V = a3 |
|
|||
|
|
|||||
|
|
|||||
|
|
|||||
|
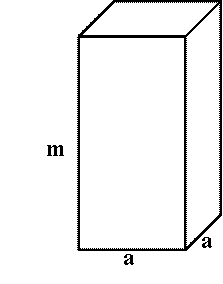
NÉGYZET ALAPÚ EGYENES HASÁB (NÉGYZETES OSZLOP)
Olyan téglatest, amelynek az
alaplapja négyzet. |
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
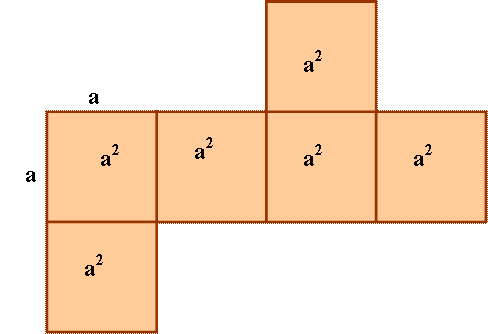
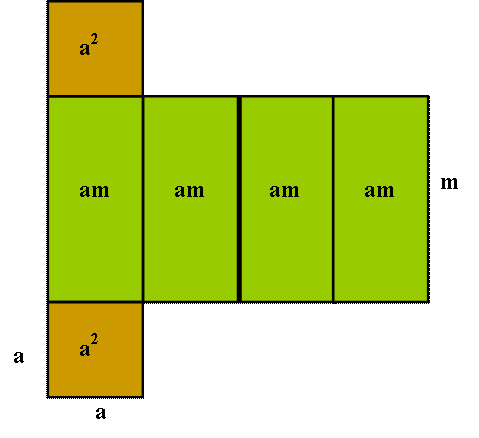
A négyzet alapú
egyenes hasáb (négyzetes oszlop)
egy lehetséges hálója. |
|||||
|
|
|||||
|
|
A
négyzetes oszlop felszíne: A = 2a2
+ 4am
A
négyzetes oszlop térfogata: V =
a2 m
|
|
|||
|
|
|||||
|
|
|||||