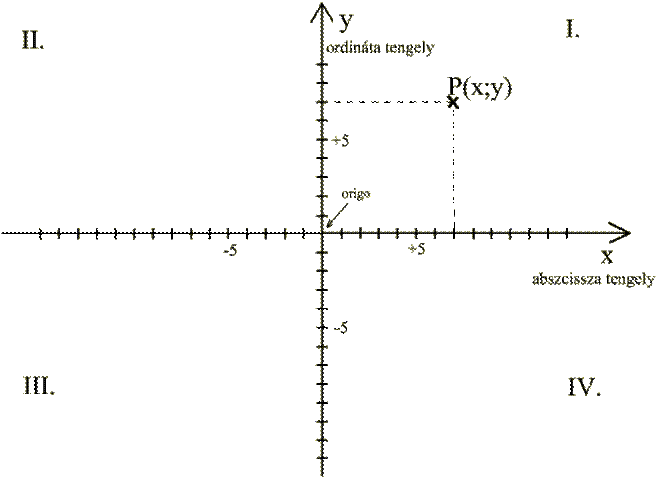|
|
|||
|
|
|||
|
|
|||
|
A derékszögű koordináta-rendszert két
egymásra merőleges számegyenes alkotja. Az egyeneseket koordinátatengelyeknek,
metszéspontjukat kezdőpontnak, origónak nevezzük. Az origóhoz mindkét számegyenesen a 0-t
rendeljük hozzá. A „vízszintes” tengely az x (abszcissza) tengely, a „függőleges” az y (ordináta) tengely. |
|||
|
|
|||
|
Az x tengelyen a számok jobbra, az y
tengelyen felfelé növekednek. |
|||
|
|
|||
|
A koordináta-rendszer segítségével a sík
bármely P pontjának a helyzete két jelzőszám (koordináta) segítségével
egyértelműen meghatározható. A pont helyzetét a két tengelytől mért előjeles
távolságával határozzuk meg. A pontnak a tengelyektől mért előjeles
távolságai a pont koordinátái (jelzőszámai). Az előjelek a számegyenesek segítségével
adhatók meg. A jelzőszámokat, a pont neve után zárójelben adjuk meg: P(x;y) |
|||
|
P(x;y) |
|||
|
|
első
jelzőszám |
második jelzőszám. |
|
|
|
|||
|
A koordináta-rendszer a síkot négy síknegyedre osztja. A negyedeket római számmal jelöljük. |
|||
|
|
|||
|
|||
|
|
|||
|
Amíg ismerkedsz a koordináta-rendszerrel,
a pontok jelzőszámainak meghatározásánál érdemes a következőképpen eljárnod:
Az origóból indulva, el kell jutnunk a kiválasztott pontba úgy, hogy csak a
tengelyekkel párhuzamosan haladhatunk, és az indulás után csak egyszer
válthatunk irányt. Az x tengelyen megtett lépések száma és iránya lesz a pont
első koordinátája. Az y tengellyel párhuzamosan megtett lépések száma és
iránya adja a pont második koordinátáját. Van még egy nagyon fontos szabály: először
mindig az x tengelyen kell elindulni. PÉLDA |
|||
|
1. |
|||
|
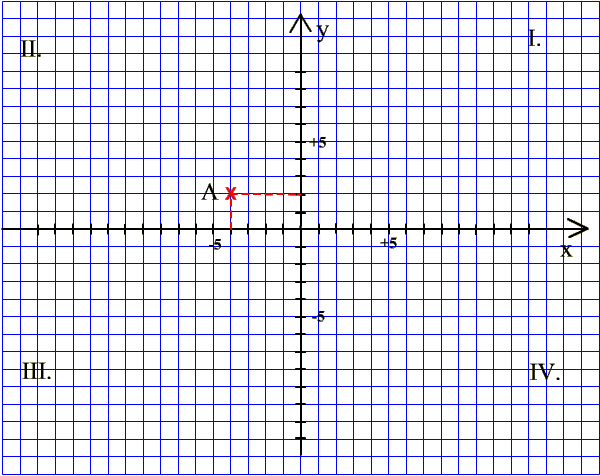
Határozzuk meg az A
pont koordinátáit! |
|
|
|
|
|
Indulás az origóból!! |
|
|
|
1. lépés x-tengelyen: negatív
irányba (balra) 4 lépés |
|
Ezért az első
jelzőszám: x = - 4 |
|
Innen tovább: |
|
2. lépés y-tengellyel párhuzamosan: pozitív irányba (fel) 2 lépés
|
|
Ezért a második
jelzőszám: y = + 2 |
|
|
|
A keresett koordináták: A(- 4;+2) |
|
|
|
|
|
2. |
|
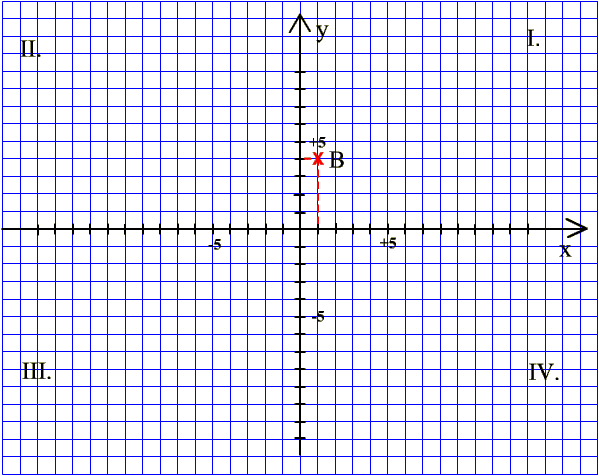
Határozzuk meg a B pont
koordinátáit! |
|
|
|
|
|
Indulás az origóból!! |
|
|
|
1. lépés x-tengelyen: pozitív
irányba (jobbra) 1 lépés |
|
Ezért az első
jelzőszám: x = + 1 |
|
Innen tovább: |
|
2. lépés y-tengellyel párhuzamosan: pozitív irányba (fel) 4 lépés
|
|
Ezért a második
jelzőszám: y = + 4 |
|
|
|
A keresett koordináták: B(+1;+4) |
|
|
|
|
|
3. |
|
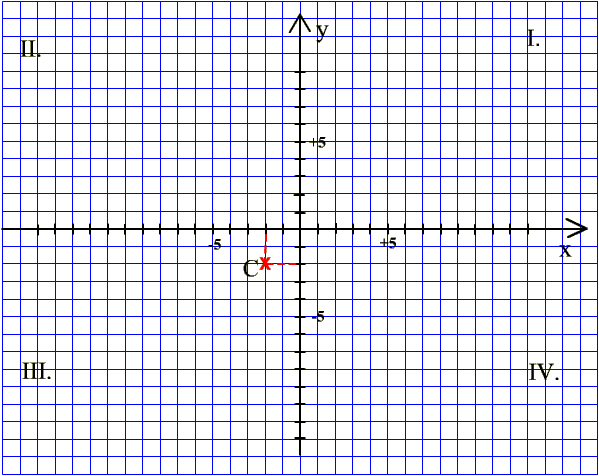
Határozzuk meg a C pont
koordinátáit! |
|
|
|
|
|
Indulás az origóból!! |
|
|
|
1. lépés x-tengelyen: negatív
irányba (balra) 2 lépés |
|
Ezért az első
jelzőszám: x = - 2 |
|
Innen tovább: |
|
2. lépés y-tengellyel párhuzamosan: negatív irányba (le) 2 lépés
|
|
Ezért a második
jelzőszám: y = - 2 |
|
|
|
A keresett koordináták: C(-2;-2) |
|
|
|
|
|
4. |
|
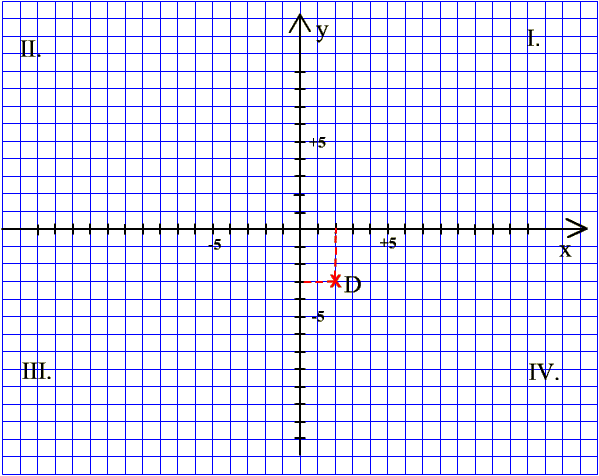
Határozzuk meg a D pont
koordinátáit! |
|
|
|
|
|
Indulás az origóból!! |
|
|
|
1. lépés x-tengelyen: pozitív
irányba (jobbra) 2 lépés |
|
Ezért az első
jelzőszám: x = + 2 |
|
Innen tovább: |
|
2. lépés y-tengellyel párhuzamosan: negatív irányba (le) 3 lépés
|
|
Ezért a második
jelzőszám: y = - 3 |
|
|
|
A keresett koordináták: D(+2;-3) |
|
|
|
|
|
5. |
|
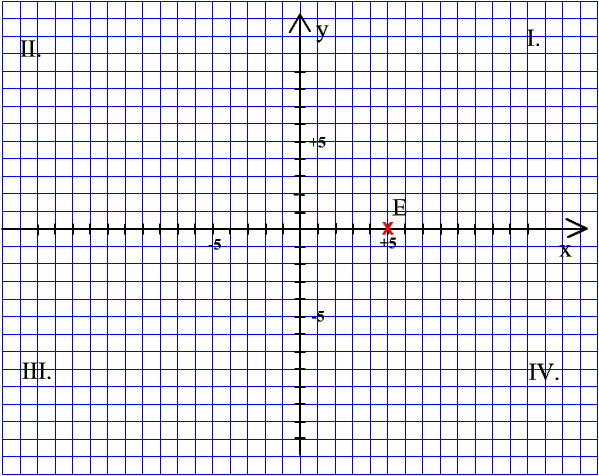
Határozzuk meg az E pont koordinátáit! |
|
|
|
|
|
Indulás az origóból!! |
|
|
|
1. lépés x-tengelyen: pozitív
irányba (jobbra) 5 lépés |
|
Ezért az első
jelzőszám: x = + 5 |
|
Innen tovább: |
|
2. lépés y-tengellyel párhuzamosan: Nem kell egyetlen lépést sem tennünk, hiszen megérkeztünk. |
|
Ezért a második
jelzőszám: y = 0 |
|
|
|
A keresett koordináták: E(+5;0) |
|
|
|
|
|
6. |
|
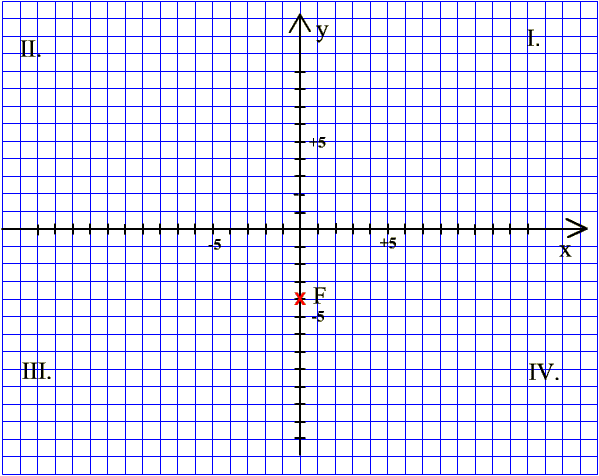
Határozzuk meg az F pont koordinátáit! |
|
|
|
|
|
Indulás az origóból!! |
|
|
|
1. lépés x-tengelyen: nem kell
egyetlen lépést sem megtenni. |
|
Ezért az első
jelzőszám: x = 0 |
|
Innen tovább: |
|
2. lépés y-tengellyel párhuzamosan: negatív irányba (lel) 4 lépés
|
|
Ezért a második
jelzőszám: y = - 4 |
|
|
|
A keresett koordináták: F(0;-4) |
|
|