Az a szög az O középpontú körnek a zölddel jelölt körívéhez tartozó középponti szöge. Ehhez a körívhez ez az egyetlen középponti szög tartozik.

Középponti szög: Olyan szög, amelynek a csúcsa a kör középpontjában van.

A körnek azt az ívét, amely a szög belsejébe esik, a középponti szöghöz tartozó körívnek nevezzük.

Egy körben, vagy egyenlő sugarú körökben

— egyenlő középponti szögekhez, egyenlő körívek tartoznak.

— egyenlő körívekhez, egyenlő középponti szögek tartoznak.

A b-val elnevezett szögek az O középpontú körnek a barnával jelölt körívéhez tartozó kerületi szögek. Végtelen sok kerületi szög tartozik a körívhez, és minden hozzá tartozó kerületi szög nagysága megegyezik.

Kerületi szög: Olyan konvex szög, amelynek a csúcsa a kör kerületén van, szárai a kör húrjai, vagy az egyik szára húr, a másik érintő.

Egy körben, vagy egyenlő sugarú körökben

— egyenlő kerületi szögekhez, egyenlő körívek tartoznak.

— egyenlő körívekhez, egyenlő kerületi szögek tartoznak.

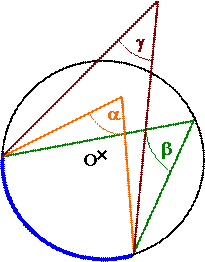
Ha egy konvex szög szárai egy körív két végpontjára illeszkednek (az ábrán látható módon), és csúcsa a körön belül van, akkor a szög nagyobb az ugyanahhoz a körívhez tartozó kerületi szögnél.

Ha egy konvex szög szárai egy körív két végpontjára illeszkednek (az ábrán látható módon), és csúcsa a körön kívül van, akkor a szög kisebb az ugyanahhoz a körívhez tartozó kerületi szögnél.

g < b < a

1.TÉTEL: (Állítás):

A kör bármely középponti szöge kétszerese az ugyanahhoz az ívhez tartozó kerületi szögnek.

Az állítást négy különböző esetre bizonyítjuk.

1.

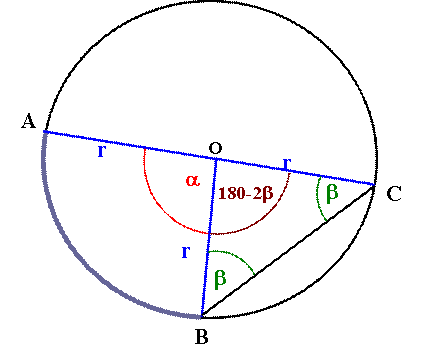
A középponti szög csúcsa a kerületi szög szögtartományába esik.

Bizonyítandó:

¨ Bizonyítás ¨

2.

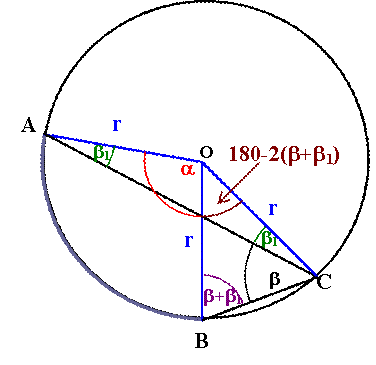
A középponti szög csúcsa a kerületi szög szárára esik.

Bizonyítandó:

¨ Bizonyítás ¨

3.

A középponti szög csúcsa a kerületi szög szögtartományán kívülre esik.

Bizonyítandó:

¨ Bizonyítás ¨

4.

A kerületi szög érintőszárú.

Bizonyítandó:

¨ Bizonyítás ¨