Gyakran csak olyan törtekkel tudunk dolgozni, amelyeknek azonos a nevezőjük (esetleg a számlálójuk). Ha mégsem azonosak a nevezők (számlálók), akkor kénytelenek vagyunk közös nevezőre (számlálóra) hozni a törteket a következőképpen:
Példa:
Hozzuk közös nevezőre a következő törteket!
; ;
1. LÉPÉS
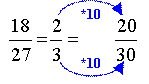
Ha lehet, egyszerűsítsük a törteket!
; ;
Az első törtet 4-gyel, a másodikat 9-cel, a harmadikat 7-tel egyszerűsítettük. A következő lépést már az egyszerűsített alakkal végezzük. Most már a törtek legegyszerűbb alakjának, keressük a közös nevezőjét.
2. LÉPÉS
Meg kell keresnünk a nevezők [6; 3; 5] legkisebb közös többszörösét. Amíg nincs nagy gyakorlatunk, érdemes a következőképpen eljárni: Írjuk egymás mellé a nevezőket. A nevezők alá, pedig a kétszeresüket, háromszorosukat stb…. Ezt mindaddig folytassuk, amíg minden nevező alatt az utolsó helyen ugyanazt a számot nem találjuk. Ez lesz a keresett közös nevező. (Mindig annál az oszlopnál kell folytatni a szorzást, ahol az utolsó helyen a legkisebb szám áll.)
	6 12 18 24 30	3 6 9 12 15 18 21 24 27 30	5 10 15 20 25 30
A közös nevező a 30.
3. LÉPÉS
Minden törtnél megkeressük az új nevezőhöz tartozó számlálót. (Bővítés)
; ;