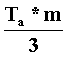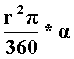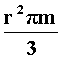|
|
||
|
|
||
|
|
||
|
|
||
|
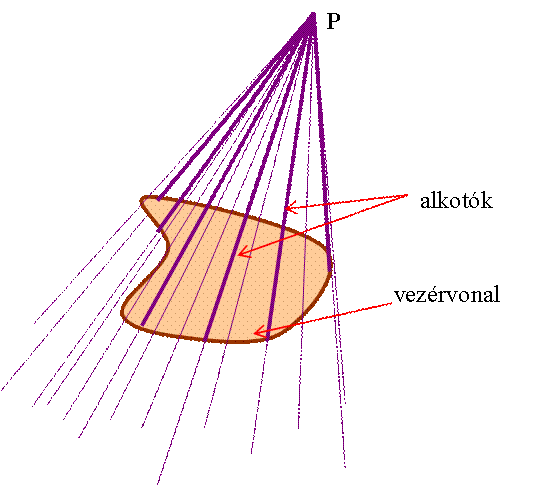
Ha egy zárt
síkidom határoló vonalának (vezérvonal) minden pontján át a síkidom síkján
kívül fekvő P pontból félegyeneseket
húzunk, akkor egy (végtelenbe nyúló) kúpfelületet
kapunk. Az adott síkidom
és a kúpfelület által határolt térrészt kúpnak
nevezzük. (Vegyük észre, hogy a gúlafelület, (gúla), olyan speciális kúpfelület, (kúp), amelynek a vezérvonala sokszöget határol!) Az adott P pontot a kúp csúcsának,
az adott síkidomot a kúp alaplapjának, a
kúpfelületnek a kúpot határoló részét a kúp palástjának,
a kúp csúcsát az alaplap határoló pontjaival összekötő szakaszokat a kúp alkotóinak nevezzük. A kúp
csúcspontjának az alaplap síkjától mért távolsága a kúp
magassága. A kúp felszíne az alaplap területének (Ta) és a palást területének (Tp) az összege: A =
Ta + Tp. A kúp térfogata az alaplapjával és a
testmagasságával megegyező alaplapú és magasságú henger térfogatának a
harmada: V = |
||
|
|
||
|
EGYENES KÖRKÚP (Forgáskúp) |
||
|
|
||
|
|
||
|
|
||
|
|
||
|
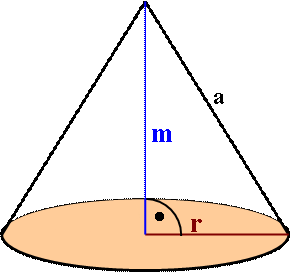
Az egyenes körkúp alaplapja kör. Az
egyenes körkúp magassága a csúcsból az alaplap középpontjába állított
merőleges szakasz. A forgáskúp alkotói egyenlő hosszúak, a csúcsot az alaplap
középpontjával összekötő szakasz merőleges az alaplap síkjára. |
||
|
|
||
|
|
||
|
|
||
|
|
||
|
Az egyenes körkúp egy lehetséges hálója. |
||
|
|
||
|
A palást olyan körcikk, amelynek köríve
olyan hosszú, mint az alaplap kerülete, sugara pedig
mint a kúp alkotója |
||
|
|
||
|
|
||
|
|
||
|
|
A kúp felszíne: A = r2 p+ rpa A = rp (r+ a) A = r2 p +
A kúp
térfogata: V = |
|
|
|
||
|
|
||