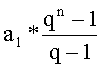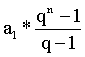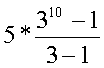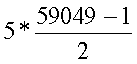|
|
|
|
|
Ha egy — 0-t nem tartalmazó — számsorozat minden tagját
osztjuk az előtte lévő taggal, és a hányados állandó, akkor a sorozat mértani
sorozat. A hányados jele: q (quotiens — kvóciens:
hányados latinul) (Másképp: Ha a számsorozat hányadossorozata
állandó, akkor a sorozat mértani sorozat.) A mértani sorozat növekvő, ha q
> 1 és a1> 0. A mértani sorozat csökkenő, ha 0 <
q < 1 és a1> 0. A mértani sorozat konstans (állandó), ha q = 1. Ha a mértani sorozat adott tagját megszorozzuk a
hányadossal, akkor a rákövetkező, ha az adott tagját elosztjuk a hányadossal,
akkor a megelőző tagot kapjuk. A mértani sorozat
tetszőleges, n-edik tagjának, első tagjának és
hányadosának kiszámítására használható képlet: an = a1
* q(n-1) A mértani sorozat tetszőleges
tagját megkapjuk, ha az első tagot megszorozzuk a hányadosnak a keresett tag
sorszámánál 1-gyel kisebb hatványával. |
|
|
|
Példa |
|
|
|
Határozzuk meg a mértani
sorozat ötödik elemét, ha ismerjük az első tagot, és hányadost! a1 = 6 q = 2 a5 = ? an = a1 * q(n-1)
a5 = 6 * 2(5-1)
a5 = 6
* 24 a5 =
96 |
|
|
|
A mértani sorozat
első n tagjának összege: Sn Sn =
Sn = a1*n ha q = 1 |
|
|
|
Bizonyítás: Bizonyítandó: Sn = Az első n tag összege: a. Sn =
a1+ a2 + a3 + . . . + an-1+ an-2 + an kifejezhető a sorozat első elemével, és
hányadosával: b. Sn =
a1+ a1 * q+ a1 * q2 + . . . + a1
* qn-2 + a1 * qn-1 // *q q ¹ 0 c. Sn
* q = a1*q + a1 * q2+ a1 *
q3 + .
. . + a1 * qn-1 +
a1 * qn A c és a b
egyenlet különbségét véve: c – b = (Sn *
q) – Sn = a1 * qn –
a1 Sn *
(q – 1) = a1 * (qn – 1) // : (q – 1) ha q ¹1 Sn = Pontosan a bizonyítandó állítást kaptuk. |
|
Példa |
|
Határozzuk meg a mértani
sorozat első 10 elemének az összegét, ha
a1 = 5 q = 3 Sn = S10 = S10 = S10 = 147620 |
|
|