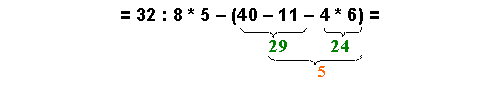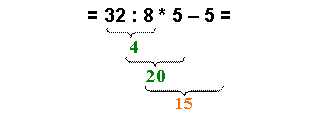Ha van zárójel
A zárójelek fajtái:		( ) kis zárójel [ ] szögletes zárójel { } kapcsos zárójel
1. LÉPÉS	A kis zárójelek között lévő műveleteket végezzük el.
2. LÉPÉS	A szögletes zárójelek között lévő műveleteket végezzük el.
3. LÉPÉS	A kapcsos zárójelek között lévő műveleteket végezzük el.
4. LÉPÉS	A megmaradt műveletek elvégzése a műveleti sorrend szabályai szerint.
A zárójelen belül a műveleti sorrend szabályai érvényesek.
Ha több azonos zárójel van a feladatban, akkor célszerű ezeket balról jobbra sorra venni. Megoldható úgy is a feladat, hogy minden lépés után a feladatot újra leírjuk, miközben minden zárójel „egyet visszalép”. Például a kapcsosból szögletes lesz. Így végül mindig a kis zárójelek közötti műveletekkel kell foglalkoznunk. Kezdő feladatmegoldónak ez a módszer megkönnyítheti a munkáját.
Példa
32 : 8 * 5 – {40 – [27 : 9 + (4 + 1) * 3 – (15 + 3 * 2) : 3] – 4 * 6}=
Az első lépésben elvégezzük a kis zárójelben lévő műveleteket, majd „visszaléptetjük” a zárójeleket. (Azokat a számokat, amelyekkel már számoltunk, akár át is húzhatjuk.)
Leírjuk a megmaradt műveleteket.
= 32 : 8 * 5 – [40 – (27 : 9 + 5 * 3 – 21 : 3) – 4 * 6] =
A második lépésben az eredetileg szögletes zárójelben lévő, műveletek következnek. A visszaléptetés miatt ezek most kis zárójelben vannak. Ne feledkezzünk meg most sem a visszaléptetésről!
Leírjuk a megmaradt műveleteket.
= 32 : 8 * 5 – (40 – 11 – 4 * 6) =
A harmadik lépésben az eredetileg kapcsos zárójelben lévő műveletek következnek. A visszaléptetés miatt ezek most kis zárójelben vannak
Leírjuk a megmaradt műveleteket.
= 32 : 8 * 5 – 5 =
Most már nincs zárójel. Alkalmazzuk a zárójel nélküli műveleti sorrend szabályait! A végeredmény:
.