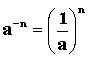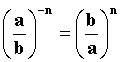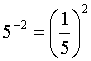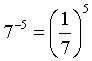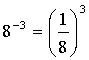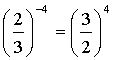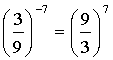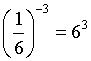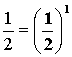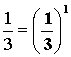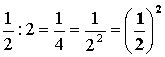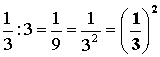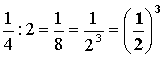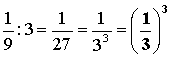|
|
||||||||||||
|
Negatív egész kitevőjű hatvány
értékét megkapjuk, ha az alap reciprok értékét, a kitevő ellentettjére
emeljük.
|
||||||||||||
|
|
||||||||||||
|
Példa |
||||||||||||
|
|
|
|
||||||||||
|
|
||||||||||||
|
|
|
|
||||||||||
|
|
||||||||||||
|
Jogos a
kérdés: Miért? Nézzünk
két konkrét példát! |
||||||||||||
|
|
||||||||||||
|
|
24
= 16 |
34
= 81 |
|
|||||||||
|
|
23
= 8 |
33
= 27 |
|
|||||||||
|
|
22
= 4 |
32
= 9 |
|
|||||||||
|
|
21
= 2 |
31
= 3 |
|
|||||||||
|
Vegyük
észre: ha a kitevőt eggyel csökkentjük, a hatványérték mindig az előző |
||||||||||||
|
|
felére |
harmadára |
|
|||||||||
|
|
változik. |
|
||||||||||
|
Csökkentsük
ismét eggyel a kitevőt, és tartsuk magunkat az előbb felismert szabályhoz! |
||||||||||||
|
|
20 = 21 :
2 = 2 : 2 = 1 |
30 = 31:3=
3 : 3 = 1 |
|
|||||||||
|
Ne álljunk meg! Csökkentsük ismét a
kitevőt, és tartsuk magunkat továbbra is az előbb már felhasznált szabályhoz! |
||||||||||||
|
|
2-1
= 1:2 = |
|
3-1
= |
|||||||||
|
|
2-2
= |
|
3-2
= |
|||||||||
|
|
2-3
= |
|
3-3
= |
|||||||||
|
Hasonlóan belátható bármely pozitív egész alap
esetén. |
||||||||||||
|
|
||||||||||||