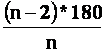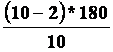Szabályos nyolcszög
A szabályos sokszög: olyan sokszög, amelynek minden oldala és minden szöge egyenlő.
TÉTEL: (Állítás):
Az n oldalú szabályos sokszög egy belső szögének nagysága: a =
Felhasználtuk, hogy a szabályos sokszög minden belső szöge egyenlő. Példa Számítsuk ki a szabályos tízszög egy szögének a nagyságát! a = = = 144°
Szabályos sokszögek szimmetriája:
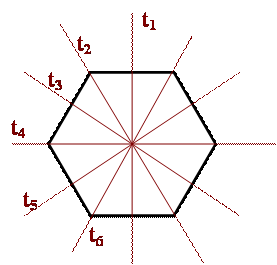
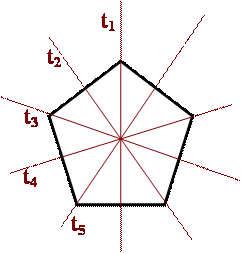
A szabályos hatszög tükörtengelyei	A szabályos ötszög tükörtengelyei
Tengelyes szimmetria: Minden szabályos sokszög tengelyesen tükrös. Minden n oldalú szabályos sokszögnek n darab tükörtengelye van. A páratlan oldalszámú szabályos sokszögek tükörtengelyei az oldalfelező merőleges egyenesek (n darab). A páros oldalszámú szabályos sokszögek tükörtengelyei az oldalfelező merőleges egyenesek (n/2 darab, mert a párhuzamos oldalak oldalfelező merőlegesei egy egyenesre esnek.), és a szögfelező egyenesek (n/2 darab, mert a szemközti szögek szögfelezői egy egyenesre esnek.).
A szabályos hatszög szimmetriaközéppontja (O)
Középpontos szimmetria: A szabályos sokszögek közül csak a páros oldalszámúak középpontosan szimmetrikusak. Az oldalfelező merőleges egyenesek metszéspontja a szimmetriaközéppont.