|
|
|
1. Állítás: |
|
|
|
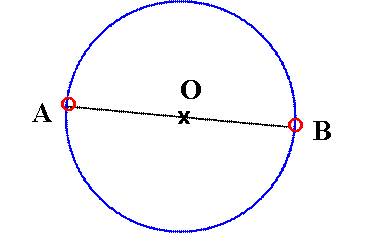
Egy AB szakasz, mint átmérő fölé
rajzolt körvonal A és B pontoktól különböző C
pontját összekötve a szakasz végpontjaival, derékszögű háromszöget
kapunk. A derékszögű csúcs mindig a C csúcs.
A kört az AB szakasz Thalesz körének
nevezzük. |
|
|
|
|
|
|
Bizonyítás
|
|
|
|
|
|
|
|
2. Állítás: |
|
|
|
Az ABC derékszögű
háromszög köré rajzolható kör középpontja az átfogó felező pontja. |
|
|
Bizonyítás
|
|
|
|
Az 1. és 2. állítás
következménye: |
|
Thalesz
tétele: A sík azon pontjainak
halmaza, mértani helye a síkon, ahonnan egy adott AB
szakasz derékszögben látszik, az AB
szakasz Thalesz köre. |
|
|
|
|
|
|
|
Az AB szakasz Thalesz köréhez a
szakasz végpontjai nem tartoznak hozzá. |
|
|