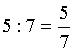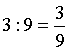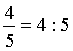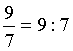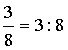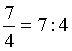El kell ismerni, hogy a közönséges tört, így első nekifutásra bizony elég kemény diónak tűnik. Szánjunk rá még egy kis időt!
Vizsgáljuk meg a következő kérdést!
Hogyan tehetünk szert csokira?
Erre a következő két módszer közül bármelyik tökéletesen megfelel:
1.
1 egész csokit felosztunk 3 egyenlő részre, és ezekből két darabot veszünk.
Legyen ez az 1 egész csoki:
Mivel csokit akarunk kapni, ezért olyan darabokra van szükségünk, aminek a neve harmad. Ehhez az 1 egész csokit 3 egyenlő részre kell felosztanunk. Osszuk fel két vágással 3 egyenlő részre!
Az 1 egész csokit felosztottuk 3 egyenlő részre. A 3 részre osztás miatt a darabok neve harmad. Az ábrán (három harmad) csoki van.
Nekünk azonban csak (kettő harmad) csokira van szükségünk, ezért a táblából csak két szelet a miénk.
Íme a csokink:
2.
Ez a módszer is csokit fog eredményezni, de itt most kicsit másképpen fogunk hozzá. Vegyünk most 2 egész csokit, és tegyük őket egymás mellé!
1 tábla csoki:
1 tábla csoki
Kerítsünk egy nagyobb kést, és két vágással osszuk el az egymás mellé tett csokikat 3 egyenlő részre!
Osszuk el most a feldarabolt csokikat 3 gyerek között egyenlően!
Gondoljuk át, mi is történt a második esetben!
2 egész csokit elosztottunk 3 felé egyenlően, és eredményül -ot kaptunk.
Írjuk le ezt a matematika nyelvén!
2 : 3 =
A 2 : 3 művelet eredménye tehát a tört.
Érdemes megjegyezni a következőket:
Minden osztás felírható közönséges tört alakban, úgy, hogy az osztandó lesz a tört számlálója, az osztó pedig a tört nevezője.
Példa
Minden közönséges tört felírható osztásként úgy, hogy a számláló lesz az osztandó, a nevező pedig az osztó.
Példa