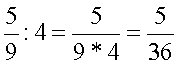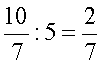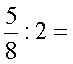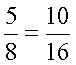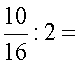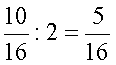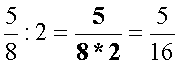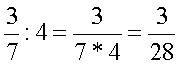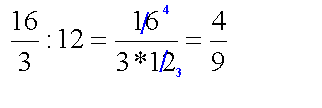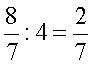Törtet úgy is oszthatunk egész számmal, hogy a nevezőt szorozzuk az osztóval, a számláló változatlan marad. (A művelet így mindig elvégezhető) A szorzás jelölése után megpróbálunk egyszerűsíteni.

Ha az osztó maradék nélkül megvan a számlálóban, akkor az osztás elvégezhető úgy is, hogy a számlálót osztjuk az osztóval, és a nevező változatlan marad.

Példa

Hogy is van ez? Nézzünk egy példát kicsit behatóbban!

Öt szelet (öt nyolcad) csokit kell egyenlően szétosztani két gyerek között. Mit tegyünk? Egyáltalán mennyi csokit kap egy-egy gyerek?

Daraboljunk fel minden szelet csokit két egyenlő részre. Így ugye most már tíz szelet csokink lesz.

Tehát:

Bővítsük az osztandót az osztóval, vagyis most 2-vel.

Írjuk az eredeti osztandó helyére a vele megegyező értékű, de új alakú osztandót!

Most tíz szelet csokit kell egyenlően szétosztani két gyerek között. Ez már nem okoz gondot. Minden gyerek kap öt szelet csokit. A szeletek neve tizenhatod.

Ezt az eredményt megkapjuk akkor is, ha az eredeti osztásban az osztandó nevezőjét megszorozzuk az osztóval.

Példa

1.

2.

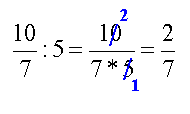
A második feladatnál a szorzás jelölése után 4-gyel egyszerűsítettünk. A számlálót (16-ot), és a nevezőben lévő szorzatban a 12-őt osztottuk 4-gyel, majd elvégeztük a nevezőben a szorzást (3 * 3).

Ahogy már említettük:

Ha a számláló osztható az osztóval, akkor az osztást úgy is elvégezhetjük, hogy a számlálót osztjuk az osztóval és a nevező változatlan marad.

Példa